|
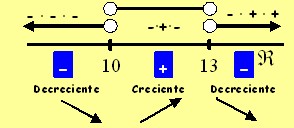
ACTIVIDAD PROPUESTA Un ayuntamiento está realizando un estudio sobre el nivel de contaminación acústica en la ciudad. Un primer plan de choque afectará a aquellos lugares donde se lleguen a superar los 65 decibelios en horario diurno. En un barrio de la ciudad se han realizado mediciones de ruido en la franja horaria más conflictiva, modelándose el nivel de ruido mediante la siguiente función (R indica el ruido en decibelios y x el tiempo entre las 9 y las 14 horas de un día laborable): R(x) = 2943 - 780x + 69x2 - 2x3 9 ≤ x ≤ 14 (a) Indica cuándo crece el nivel de ruido y cuándo decrece. (b) Dibuja la gráfica de la función. ¿Se debería iniciar un plan de choque en este barrio? RESOLUCIÓN MÉTODO 1: RESOLUCIÓN MEDIANTE EL ESTUDIO LOCAL DE FUNCIONES A TRAVÉS DE DERIVADAS x: "tiempo ente las 9 y las 14 horas en un día laborable" R(x): "Ruido expresado en decibelios". R(x) = 2943 - 780x + 69x2 - 2x3 9 ≤ x ≤ 14 RESOLUCIÓN apartado (a) Vamos a estudiar el crecimiento de la función; para ello estudiaremos su derivada primera: R(x) sea estrictamente creciente à R'(x) > 0 ; R(x) sea estrictamente decreciente à R'(x) < 0 R'(x) = - 780 + 138x - 6x2 9 ≤ t ≤ 14 Estudiamos el signo de dicha expresión para lo que factorizamos: - 780 + 138x - 6x2 = 0 x1 = 10 ; x2 = 13 - 6 (x - 10) (x - 13) Estudiamos el signo de la función en cada uno de estos 3 intervalos que determinan estos dos valores
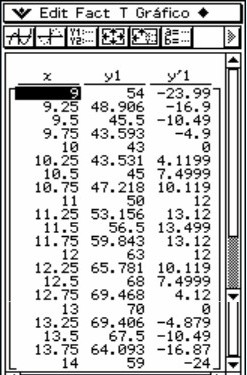
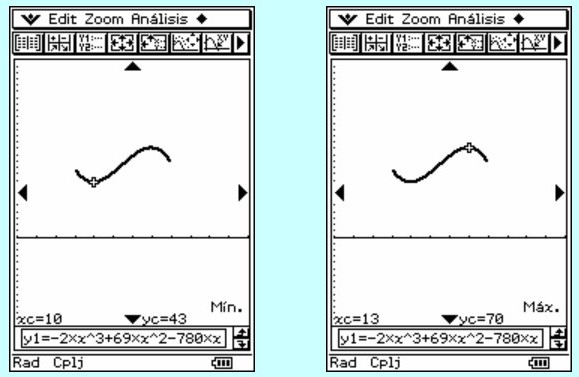
Para 9 ≤ t ≤ 14, la función será decreciente a partir de las 9 hasta llegar a as 10, momento en el que el ruido empezará a ser creciente hasta llegar a las 13 horas. A partir de las 13 horas irá decreciendo hasta las 14 horas, a partir de cuyo momento el estudio deja de hacerse. De esto deducimos que en x = 10 hay un mínimo relativo y en x = 13 hay un máximo relativo. Con la ayuda de una tabla de valores y los datos anteriormente calculados podemos hacer un esbozo de gráfica. Mínimo (10, 43) Máximo (13, 70)
Como vemos, e xiste una amplia variedad de problemas y aplicaciones que tienen las siguientes finalidades:- E ncontrar el área mínima o la máxima.- La menor resistencia - El mayor alcance - El menor coste. - El mayor beneficio. - La forma óptima. Todos estos problemas, se engloban dentro de la categoría de Optimización de funciones. 1.- Identificar las variables del enunciado. 2.- Identificar las cantidades dadas y las que hay que determinar, con sus respectivas unidades. 3.- Plantear la función que hay que maximizar o minimizar. 4.- Comprobar cuántas variables independientes tiene: (a) Si tiene sólo una proseguir el problema. (B) En caso de tener 2 ó más, buscar ecuaciones secundarias que relacionen las variables y sustituirla en la función de modo que nos quede una sola variable. 5.- Derivar la función e igualarla a cero, para hallar los extremos locales. 6.- Realizar la 2ª derivada para comprobar el resultado obtenido. 7.- Observar el dominio del problema, los valores para los que tiene sentido.
|