|
MOEBIUS (1995) Ficha técnica Duración: 01:27:44 Director: Gustavo Mosquera Intérpretes: Guillermo Angelelli (Daniel Pratt), Roberto Carnaghi (Marcos Biasi), Jorge Petraglia (Mistein), Anabella Levy (Abril), Miguel Ángel Paludi (Aguirre), Fernando Llosa (Nazar), Martín Adjemian (Canotti), Daniel Dibiase (Kenn) Estreno: lunes 1 enero 1996 Género: Ciencia ficción Fama Films |
|
|
|
Plantea una situación inexplicable, con trasfondo matemático y metáfora filosófica incluida, aunque en este caso no hay Matemáticas explícitas, sólo referencias a la banda de Moebius y a alguna de sus propiedades |
|
Sinopsis (Advertencia: Esta sección contiene detalles de la trama y el argumento)
|
En esta película iremos intercalando escenas de contenido matemático con la sinopsis: Fidelísima adaptación del estupendo cuento “Un túnel llamado Moebius” (1950), del astrónomo Armin Joseph Deutsch. Un tren del Metro de Buenos Aires, el 86, desaparece inexplicablemente con más de 30 pasajeros. Los conductores de otras líneas creen oírlo, de hecho los sistemas de seguridad detectan su presencia en diferentes ocasiones, pero nadie consigue verlo, ni saber dónde está.
Los responsables del “Subte”, como se llama al metro en Argentina, y las autoridades tratarán de resolver el enigma antes de que la opinión pública se entere del asunto. En principio tratan de ponerse en contacto con el ingeniero que supervisó las obras de ampliación del Metro. Pero, apurado por los plazos de ejecución de otra obra, contacta con Daniel Pratt, un joven matemático, topólogo, del que tiene referencias. Una vez más, el poder urge soluciones y la ciencia desvela complejidades.
- Le llamé a usted que le gustan los problemas -comenta irónicamente el ingeniero del metro. El nivel de sarcasmo de la práctica totalidad de los diálogos es muy elevado. Entonces Pratt, al conocer el asunto, le replica que él es topólogo. - ¡Ah! La fascinación por el análisis de las superficies -replica el ingeniero, y añade - Ustedes los matemáticos ... , una fórmula, un cálculo, y lo guardan en el fondo de un libro. Una vez designado para resolver el asunto, Pratt se presenta ante el director del Metro, Marcos Blasi, contrariado porque no es la persona que esperaba:
- Me dieron las instrucciones para solucionar lo que necesita. - Pero si usted no tiene ni idea de lo que se trata. - ¿Un matemático? ¿para qué sirve eso? ¿para qué quiero yo un matemático? - Soy topólogo. Matemático. - ¿Para qué sirve eso?. - Es una rama de las Matemáticas que investiga las superficies... y las convierte en fórmulas. - ¡Muy útil para mis nervios! ¡Esto es el colmo!. Haciendo honor a su especialidad, lo primero que se le ocurre es consultar los planos del “perimetral”. Y como usualmente ocurre, los planos no aparecen donde deberían estar. Pratt se escandaliza: - Los planos originales no se pueden retirar - a lo que el anciano archivero replica - Depende de quien los pida.
Para localizar los planos, sus pesquisas le llevan a un antiguo profesor suyo de Matemáticas de la facultad. Cuando Pratt llega allí, asistimos al final de una clase de una profesora, de la Cátedra de topología, ante no más de una veintena de alumnos, sobre espacios topológicos. Hace una reflexión final que nos da pistas sobre lo que va a ocurrir: - Cualquiera que dijera que ciertas regiones del tiempo se paralizan, habría que, por lo menos, escucharlo. Puede que tenga razón.
Al preguntarle sobre el paradero del viejo profesor a cargo de la cátedra, se sorprende e informa a Pratt que hacía años que no daba clase: - Estaba abstraído, había perdido el interés por las clases. Tenía la cabeza en otra cosa.
Momento en el que Daniel Pratt se percata de cuál puede ser el problema: alguien ha construido sobre las vías del metro una banda de Moebius. - Este tren, en algún punto de su recorrido, se esfumó. Dio con un nodo, que en el campo de la topología es una particularidad, un polo de orden superior. El sistema perimetral es una red de asombrosa complejidad topológica, llevando a la conectividad de todo el sistema a un orden tal alto que no sé cómo calcularlo, supongo que ha llegado a ser infinito. De ser así podríamos deducir que el sistema se comporta como una cinta de Moebius -comenta, mientras describe cómo se construye una cinta de Moebius.
- ¿Podrían imaginarse las infinitas propiedades matemáticas existentes? - ¿Ésta es la posible explicación? ¡Usted es un desubicado! - Es una desgracia que no haya nadie que pueda dar una explicación coherente. - Oiga, señor matemático, no quiero verle más por aquí. Los momentos de investigaciones matemáticas se suceden en poco tiempo; son análisis convulsivos, nerviosos, estereotipo al que ya estamos habituados, lejos de la realidad del trabajo diario y método del matemático.
Finalmente se encuentra con su viejo profesor desaparecido, en otra dimensión, en ese tren fantasma, en otro tiempo, en fecha diferente, en una nueva alusión a la tan deseada cuarta dimensión, harto de repetir las mismas frases, las mismas ideas, sin ser escuchado, explicando aquello que no quieren entender.
Las frases se suceden, la Filosofía aflora, la mezcla de imágenes en diferentes tiempos se observan. Realmente destacan multitud de diálogos "matemático - filosóficos" que no hacen sino resaltar el carácter abstracto de nuestra querida ciencia, además de interesantes las reflexiones sobre la sociedad actual, sobre las no resueltas desapariciones durante la dictadura argentina, finalizando la película con el anuncio cíclico de una nueva desaparición: - El hombre ha inventado numerosas máquinas, pero él mismo olvida que es una máquina mucho más complicada que todas las que ha inventado. - El hombre no conoce ni hasta qué punto no se conoce. - Nadie puede enfrentarse al infinito sin sentir vértigo. - Vivimos en un mundo en el que ya nadie escucha. - Nos estamos moviendo a la velocidad del pensamiento. - Viajamos a una velocidad imposible. - Un simple cambio de vías. El tren cruzó un empalme después de una curva. La combinación justa, en el momento adecuado, para aplicar las propiedades: una cinta de Moebius. - ¿Cómo puede ser que una superficie finita se convierta en infinita?
Destaca el uso de la perspectiva y la entrada en campo de diversos personajes, resaltando de continuo el contraste en la variedad de planos focales, produciendo, mediante este efecto óptico, un juego de contrastes, en su selección de objetivos y subrayando de tal modo lo que plantea la película en su fondo: el encuentro entre dos concepciones antitéticas, dos universos alternos que coinciden en un punto que sirve de cruce entre éste y aquél. Ese subrayado se acentúa también con una serie de metáforas visuales: La más patente de las cuales sería esa montaña rusa que reproduce la figura de una cinta de Moebius:
El plano al que sigue de inmediato un calendario que muestra un inmenso 8, otra representación de la cinta, que inclinado ofrecerá el emblema del infinito, un plano en contrapicado de una carretera escindida, rota, que no conduce a lugar alguno.
La cinta de Moebius
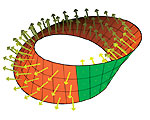
x(u,v) = [1 + (v/2) cos (u/2)]· cos u y(u,v) = [1 + (v/2) cos (u/2)]· sen u z(u,v) = (v/2) sin (u/2)
x = cos u + v cos (u/2)· cos u y = sen u + v cos (u/2)· sen u z = v sin (u/2)
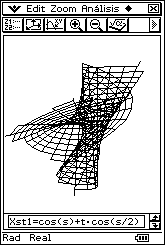
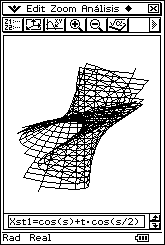
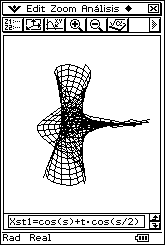
donde 0 ≤ u < 2π y - 1 ≤ v ≤ 1 Esto produce una banda de Möbius de ancho unitario, cuya circunferencia central tiene radio unitario y se encuentra en el plano coordenado x-y centrada en (0,0,0). El parámetro u recorre la banda mientras v se desplaza de un borde a otro. La banda de Möbius o cinta de Möbius (pronunciado en español a menudo "moebius", pero nunca "mobius") es una superficie con un solo lado y un solo componente de contorno. Tiene la propiedad matemática de ser un objeto no orientable. También es una superficie reglada. Fue codescubierta en forma independiente por los matemáticos alemanes August Ferdinand Möbius y Johann Benedict Listing en 1858. La banda de Möbius tiene una serie de propiedades curiosas: Para construirla se parte de una cinta cerrada de dos componentes en la frontera (un cilindro Sl x I), se hace un corte (entre las dos fronteras), se gira 180° uno de los extremos y se vuelve a pegar. La banda resultante tiene sólo un borde, lo que se puede comprobar siguiendo el borde con un dedo, por ejemplo, y notando que se alcanza el punto opuesto sin haber atravesado la superficie; asimismo, si se trata de pintar un lado de un color y el opuesto de otro, se llegará al momento en que los dos colores choquen. Si se parte con una díada (pareja) de ejes perpendiculares, y se desplaza paralelamente a lo largo de la cinta, se llegará al punto de partida con la orientación invertida. Este objeto se utiliza frecuentemente como ejemplo en topología. Constituye una de las paradojas geométricas más célebres y comprensibles inmediatamente. Una forma de representar la banda de Möbius (cerrada y con frontera) como un subconjunto de R3 es mediante la parametrización: Aplicaciones en la vida cotidiana. - En un casete de audio, de los que se usan en los grabadores comunes, entran en una especie de loop o lazo, el tape está enrollado como una cinta de Moebius. En ellos, se puede grabar de los dos “lados”, y el aprovechamiento mayor de su capacidad es obvio. - Hay ciertas impresoras que funcionan a tinta o las viejas máquinas de escribir, solían tener enrollada la cinta que va dentro del cartucho formando una banda de Moebius. - Por último, una curiosidad más: Elizabeth Zimmerman diseñó unas bufandas aprovechando las cintas de Moebius e hizo una fortuna con sus tejidos. El interés en las bandas de Moebius no pasa sólo por sus aplicaciones, reales o potenciales. Pasa por la imaginación y el descubrimiento de algo que ahora parece sencillo y obvio. Hace un poquito más de un siglo y medio, no lo era y es producto de hacer matemática. Comentario. La película es el ejercicio efectuado por un conjunto de 45 estudiantes y algunos de sus profesores de la Universidad del Cine de Buenos Aires. Con un escasísimo presupuesto, ha ganado diversos premios: en el Festival de Cine de La Habana de 1996: mejor fotografía y mejor sonido (Martín Grignaschi); en el Festival de Cine Hispano de Miami de 1996: mejor guión; en la Vienale de 1997, el premio FIPRESCI a su realizador Gazapos Escena: 0:09:43 - 0:12:33 Cuando le regalan al protagonista un juego topológico pregunta: - Y esto... ¿para qué sirve?. - No lo sé, dicen que potencia la percepción, ¡resuélvalo!.
¿Cómo un topólogo no va a saber lo que es un juego topológico? |
|
|
© Abel Martín & Marta Martín Sierra Esta página WEB se dedica exclusivamente a fines educativos, relacionando las "Matemáticas y el Cine". No existe ningún interés lucrativo. Las imágenes han sido tomadas de la TV y de Internet.
|
